publications
publications by categories in reversed chronological order
2025
- Reprogrammable Mechanical Metamaterials via Passive and Active Magnetic InteractionsC. Perez-Garcia, R. Zaera, J. Aranda-Ruiz, G. Bordiga, G. Risso, M. L. Lopez-Donaire, K. Bertoldi, and D. Garcia-GonzalezAdvanced Materials, Apr 2025
This study experimentally demonstrates the reprogrammability of a rotating-squares-based mechanical metamaterial with an embedded array of permanent magnets. How the orientation, residual magnetization, and stiffness of the magnets influence both the static and dynamic responses of the metamaterial is systematically investigated. It is showed that by carefully tuning the magnet orientation within the metamaterial, notable tunability of the metamaterial response can be achieved across static and dynamic regimes. More complex magnetic node configurations can optimize specific structural responses by decoupling the tunability of quasi-static stress–strain behavior from energy absorption under impact loading. Additionally, reprogrammability can be further enhanced by an external magnetic field, which modulates magnetic interactions within the structure. This work paves the way for developing engineered structural components with adaptable mechanical responses, reprogrammable through either the redistribution of magnetic elements or the application of an external magnetic field.
@article{perez-garcia2025reprogrammable, title = {Reprogrammable {{Mechanical Metamaterials}} via {{Passive}} and {{Active Magnetic Interactions}}}, author = {{Perez-Garcia}, C. and Zaera, R. and {Aranda-Ruiz}, J. and Bordiga, G. and Risso, G. and {Lopez-Donaire}, M. L. and Bertoldi, K. and {Garcia-Gonzalez}, D.}, year = {2025}, month = apr, journal = {Advanced Materials}, pages = {2412353}, issn = {1521-4095}, doi = {10.1002/adma.202412353}, }
2024
- Automated Discovery of Reprogrammable Nonlinear Dynamic MetamaterialsG. Bordiga, E. Medina, S. Jafarzadeh, C. Bösch , R. P. Adams, V. Tournat, and K. BertoldiNature Materials, Sep 2024
Harnessing the rich nonlinear dynamics of highly deformable materials has the potential to unlock the next generation of functional smart materials and devices. However, unlocking such potential requires effective strategies to spatially engineer material architectures within the nonlinear dynamic regime. Here we introduce an inverse-design framework to discover flexible mechanical metamaterials with a target nonlinear dynamic response. The desired dynamic task is encoded via optimal tuning of the full-scale metamaterial geometry through an inverse-design approach powered by a fully differentiable simulation environment. By deploying such a strategy, mechanical metamaterials are tailored for energy focusing, energy splitting, dynamic protection and nonlinear motion conversion. Furthermore, our design framework can be expanded to automatically discover reprogrammable architectures capable of switching between different dynamic tasks. For instance, we encode two strongly competing tasks—energy focusing and dynamic protection—within a single architecture, using static precompression to switch between these behaviours. The discovered designs are physically realized and experimentally tested, demonstrating the robustness of the engineered tasks. Our approach opens an untapped avenue towards designer materials with tailored robotic-like reprogrammable functionalities.
@article{bordiga2024automated, title = {Automated Discovery of Reprogrammable Nonlinear Dynamic Metamaterials}, author = {Bordiga, G. and Medina, E. and Jafarzadeh, S. and B{\"o}sch, C. and Adams, R. P. and Tournat, V. and Bertoldi, K.}, year = {2024}, month = sep, journal = {Nature Materials}, volume = {23}, number = {11}, pages = {1486--1494}, issn = {1476-4660}, doi = {10.1038/s41563-024-02008-6}, } - Liquid Crystal Elastomer Lattices with Thermally Programmable Deformation via Multi-Material 3D PrintingA. Kotikian, A. A. Watkins, G. Bordiga, A. Spielberg, Z. S. Davidson, K. Bertoldi, and J. A. LewisAdvanced Materials, Jan 2024
An integrated design, modeling, and multi-material 3D printing platform for fabricating liquid crystal elastomer (LCE) lattices in both homogeneous and heterogeneous layouts with spatially programmable nematic director order and local composition is reported. Depending on their compositional topology, these lattices exhibit different reversible shape-morphing transformations upon cycling above and below their respective nematic-to-isotropic transition temperatures. Further, it is shown that there is good agreement between their experimentally observed deformation response and model predictions for all LCE lattice designs evaluated. Lastly, an inverse design model is established and the ability to print LCE lattices with the predicted deformation behavior is demonstrated. This work opens new avenues for creating architected LCE lattices that may find potential application in energy-dissipating structures, microfluidic pumping, mechanical logic, and soft robotics.
@article{kotikian2024liquid, title = {Liquid Crystal Elastomer Lattices with Thermally Programmable Deformation via Multi-Material {{3D}} Printing}, author = {Kotikian, A. and Watkins, A. A. and Bordiga, G. and Spielberg, A. and Davidson, Z. S. and Bertoldi, K. and Lewis, J. A.}, year = {2024}, month = jan, journal = {Advanced Materials}, pages = {2310743}, issn = {1521-4095}, doi = {10.1002/adma.202310743}, } - Textile Hinges Enable Extreme Properties of Kirigami MetamaterialsA. S. Meeussen, G. Bordiga, A. X. Chang, B. Spoettling, K. P. Becker, L. Mahadevan, and K. BertoldiAdvanced Functional Materials, Nov 2024
Mechanical metamaterials – structures with unusual properties that emerge from their internal architecture – that are designed to undergo large deformations typically exploit large internal rotations, and therefore, necessitate the incorporation of flexible hinges. In the mechanism limit, these metamaterials consist of rigid bodies connected by ideal hinges that deform at zero energy cost. However, fabrication of structures in this limit has remained elusive. Here, we demonstrate that the fabrication and integration of textile hinges provides a scalable platform for creating large structured metamaterials with mechanism-like behaviors. Further, leveraging recently introduced kinematic optimization tools, we demonstrate that textile hinges enable extreme shape-morphing responses, paving the way for the development of the next generation of mechanism-based metamaterials.
@article{meeussen2024textile, title = {Textile Hinges Enable Extreme Properties of Kirigami Metamaterials}, author = {Meeussen, A. S. and Bordiga, G. and Chang, A. X. and Spoettling, B. and Becker, K. P. and Mahadevan, L. and Bertoldi, K.}, year = {2024}, month = nov, journal = {Advanced Functional Materials}, pages = {2415986}, doi = {10.1002/adfm.202415986}, }
2022
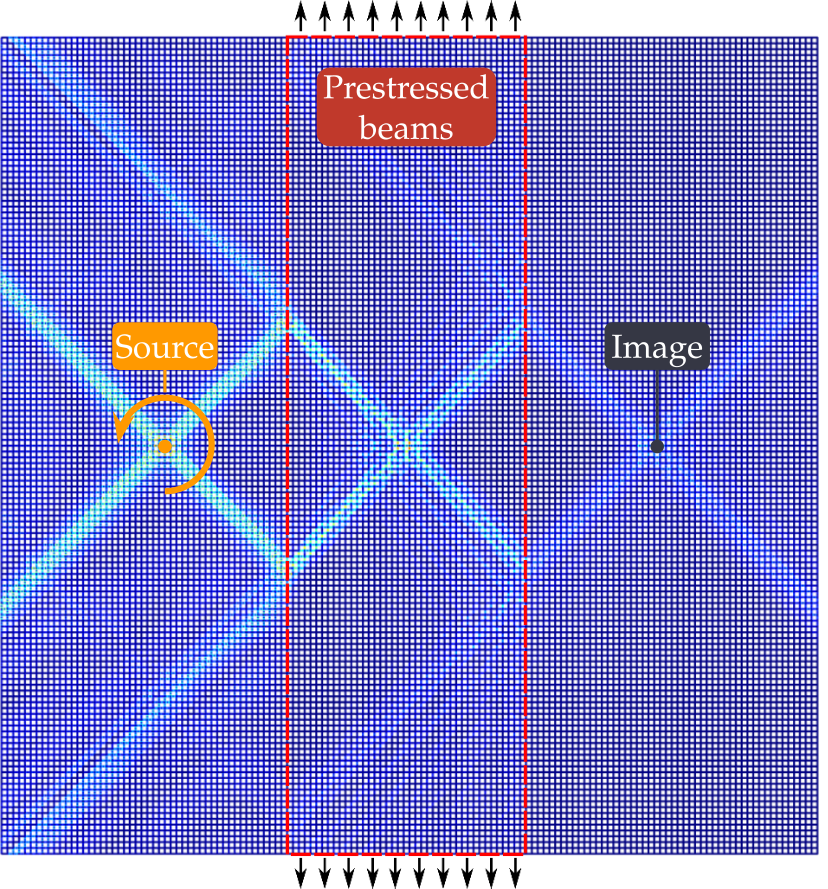
- Tensile Material Instabilities in Elastic Beam Lattices Lead to a Bounded Stability DomainG. Bordiga, D. Bigoni, and A. PiccolroazPhilosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, Sep 2022
Homogenization of the incremental response of grids made up of preloaded elastic rods leads to homogeneous effective continua which may suffer macroscopic instability, occurring at the same time in both the grid and the effective continuum. This instability corresponds to the loss of ellipticity in the effective material and the formation of localized responses as, for instance, shear bands. Using lattice models of elastic rods, loss of ellipticity has always been found to occur for stress states involving compression of the rods, as usually these structural elements buckle only under compression. In this way, the locus of material stability for the effective solid is unbounded in tension, i.e. the material is always stable for a tensile prestress. A rigorous application of homogenization theory is proposed to show that the inclusion of sliders (constraints imposing axial and rotational continuity, but allowing shear jumps) in the grid of rods leads to loss of ellipticity in tension so that the locus for material instability becomes bounded. This result explains (i) how to design elastic materials subject to localization of deformation and shear banding for all radial stress paths; and (ii) how for all these paths a material may fail by developing strain localization and without involving cracking. This article is part of the theme issue ‘Wave generation and transmission in multi-scale complex media and structured metamaterials (part 1)’.
@article{bordiga2022tensile, title = {Tensile Material Instabilities in Elastic Beam Lattices Lead to a Bounded Stability Domain}, author = {Bordiga, G. and Bigoni, D. and Piccolroaz, A.}, year = {2022}, month = sep, journal = {Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences}, volume = {380}, number = {2231}, pages = {20210388}, doi = {10.1098/rsta.2021.0388}, addendum = {(Cover article)}, } - A Way to Hypo-Elastic Artificial Materials without a Strain Potential and Displaying Flutter InstabilityG. Bordiga, A. Piccolroaz, and D. BigoniJournal of the Mechanics and Physics of Solids, Jan 2022
Cauchy-elastic solids include hyper-elasticity and a subset of elastic materials for which the stress does not follow from a scalar strain potential. More in general, hypo-elastic materials are only defined incrementally and comprise Cauchy-elasticity. Infringement of the hyper-elastic ‘dogma’ is so far unattempted and normally believed to be impossible, as it apparently violates thermodynamics, because energy may be produced in closed strain cycles. Contrary to this belief, we show that non-hyper-elastic behavior is possible and we indicate the way to a practical realization of this new concept. In particular, a design paradigm is established for artificial materials where follower forces, so far ignored in homogenization schemes, are introduced as loads prestressing an elastic two-dimensional grid made up of linear elastic rods (reacting to elongation, flexure and shear). A rigorous application of Floquet–Bloch wave asymptotics yields an unsymmetric acoustic tensor governing the incremental dynamics of the effective material. The latter is therefore the incremental response of a hypo-elastic solid, which does not follow from a strain potential and thus does not belong to hyper-elasticity. Through the externally applied follower forces (which could be originated via interaction with a fluid, or a gas, or by application of Coulomb friction, or non-holonomic constraints), the artificial material may adsorb/release energy from/to the environment, and therefore produce energy in a closed strain loop, without violating any rule of thermodynamics. The solid is also shown to display flutter, a material instability corresponding to a Hopf bifurcation, which was advocated as possible in plastic solids, but never experimentally found and so far believed to be impossible in elasticity. The discovery of elastic materials capable of sucking up or delivering energy in closed strain cycles through interaction with the environment paves the way to realizations involving micro and nano technologies and finds definite applications in the field of energy harvesting.
@article{bordiga2022way, title = {A Way to Hypo-Elastic Artificial Materials without a Strain Potential and Displaying Flutter Instability}, author = {Bordiga, G. and Piccolroaz, A. and Bigoni, D.}, year = {2022}, month = jan, journal = {Journal of the Mechanics and Physics of Solids}, volume = {158}, pages = {104665}, issn = {0022-5096}, doi = {10.1016/j.jmps.2021.104665}, }
2021
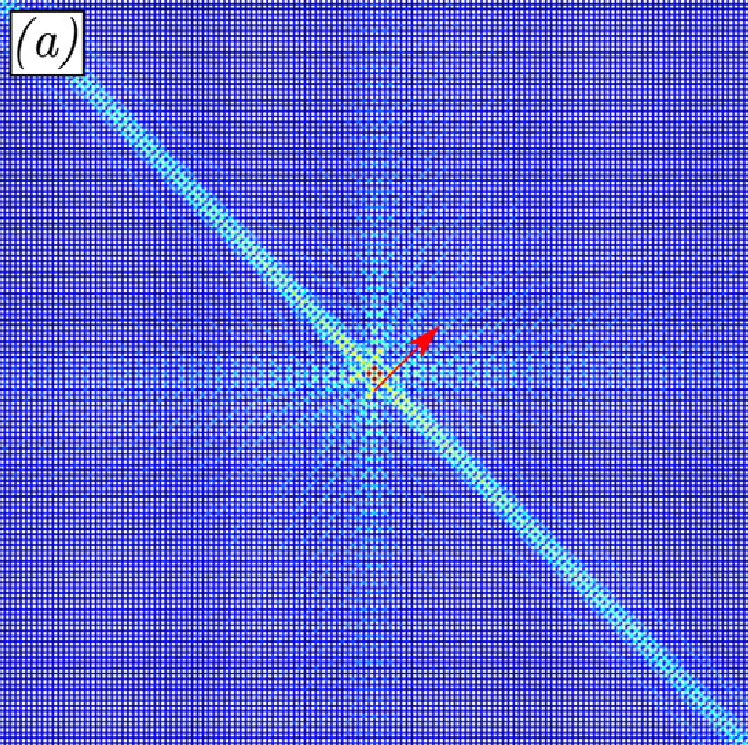
- Dynamics of Prestressed Elastic Lattices: Homogenization, Instabilities, and Strain LocalizationG. Bordiga, L. Cabras, A. Piccolroaz, and D. BigoniJournal of the Mechanics and Physics of Solids, Jan 2021
A lattice (or ‘grillage’) of elastic Rayleigh rods (possessing a distributed mass density, together with rotational inertia) organized in a parallelepiped geometry can be axially loaded up to an arbitrary amount without distortion and then be subject to incremental time-harmonic dynamic motion. At certain threshold levels of axial load, the grillage manifests instabilities and displays non-trivial axial and flexural incremental vibrations. Including every possible structural geometry and for an arbitrary amount of axial stretching, Floquet–Bloch wave asymptotics is used to homogenize the in-plane mechanical response, so to obtain an equivalent prestressed elastic solid subject to incremental time-harmonic vibration, which includes, as a particular case, the incremental quasi-static response. The equivalent elastic solid is obtained from its acoustic tensor, directly derived from homogenization and shown to be independent of the rods’ rotational inertia. Loss of strong ellipticity in the equivalent continuum coincides with macro-bifurcation in the lattice, while micro-bifurcation remains undetected in the continuum and corresponds to a vibration of vanishing frequency of the lowest dispersion branch of the lattice, occurring at finite wavelength. Dynamic homogenization reveals the structure of the acoustic branches close to ellipticity loss and the analysis of forced vibrations (both in physical space and Fourier space) shows low-frequency wave localizations. A perturbative approach based on dynamic Green’s function is applied to both the lattice and its equivalent continuum. This shows that only macro-instability corresponds to localization of incremental strain, while micro-instabilities occur in modes which spread throughout the whole lattice with an ‘explosive’ character. In particular, extremely localized mechanical responses are found both in the lattice and in the solid, with the advantage that the former can be easily realized, for instance via 3D printing. In this way, features such as shear band inclination, or the emergence of a single shear band, or competition between micro and macro instabilities become all designable features. The comparison between the mechanics of the lattice and its equivalent solid shows that the homogenization technique allows an almost perfect representation, except when micro-bifurcation is the first manifestation of instability. Therefore, the presented results pave the way for the design of architected cellular materials to be used in applications where extreme deformations are involved.
@article{bordiga2021dynamics, title = {Dynamics of Prestressed Elastic Lattices: {{Homogenization}}, Instabilities, and Strain Localization}, shorttitle = {Dynamics of Prestressed Elastic Lattices}, author = {Bordiga, G. and Cabras, L. and Piccolroaz, A. and Bigoni, D.}, year = {2021}, month = jan, journal = {Journal of the Mechanics and Physics of Solids}, volume = {146}, pages = {104198}, issn = {0022-5096}, doi = {10.1016/j.jmps.2020.104198}, }
2019
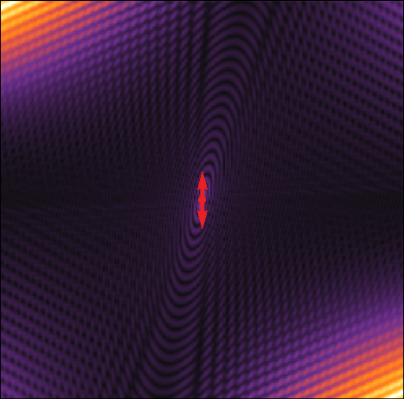
- Free and Forced Wave Propagation in a Rayleigh-beam Grid: Flat Bands, Dirac Cones, and Vibration Localization vs IsotropizationG. Bordiga, L. Cabras, D. Bigoni, and A. PiccolroazInternational Journal of Solids and Structures, Apr 2019
In-plane wave propagation in a periodic rectangular frame structure, which includes axial and flexural deformation, the latter enhanced with rotational inertia (so-called ‘Rayleigh beams’), is analyzed both with a Floquet-Bloch exact formulation for free oscillations and with a numerical treatment (developed with PML absorbing boundary conditions) for forced vibrations (including Fourier representation and energy flux evaluations), induced by a concentrated force or moment. A complex interplay is observed between axial and flexural vibrations (not found in the common idealization of out-of-plane motion), giving rise to several forms of vibration localization: ‘X-’, ‘cross-’ and ‘star-’ shaped, and channel propagation. These localizations are triggered by several factors, including rotational inertia and slenderness of the beams and the type of forcing source (concentrated force or moment). Although the considered grid of beams introduces an orthotropy in the mechanical response, a surprising ‘isotropization’ of the vibration is observed at special frequencies. Moreover, rotational inertia is shown to ‘sharpen’ degeneracies related to Dirac cones (which become more pronounced when the aspect ratio of the grid is increased), while the slenderness can be tuned to achieve a perfectly flat band in the dispersion diagram. The obtained results can be exploited in the realization of metamaterials designed to filter waves during propagation.
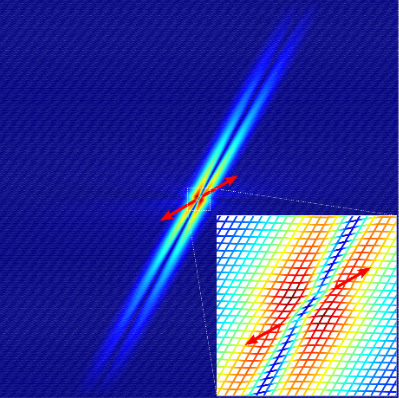
@article{bordiga2019free, title = {Free and Forced Wave Propagation in a {{Rayleigh-beam}} Grid: {{Flat}} Bands, {{Dirac}} Cones, and Vibration Localization vs Isotropization}, shorttitle = {Free and Forced Wave Propagation in a {{Rayleigh-beam}} Grid}, author = {Bordiga, G. and Cabras, L. and Bigoni, D. and Piccolroaz, A.}, year = {2019}, month = apr, journal = {International Journal of Solids and Structures}, volume = {161}, pages = {64--81}, issn = {0020-7683}, doi = {10.1016/j.ijsolstr.2018.11.007}, } - Prestress Tuning of Negative Refraction and Wave Channeling from Flexural SourcesG. Bordiga, L. Cabras, A. Piccolroaz, and D. BigoniApplied Physics Letters, Jan 2019
The quest for wave channeling and manipulation has driven a strong research effort on topological and architected materials, capable of propagating localized electromagnetical or mechanical signals. With reference to an elastic structural grid, the elements of which can sustain both axial and flexural deformations, it is shown that material interfaces can be created with structural properties tuned by prestress states to achieve total reflection, negative refraction, and strongly localized signal channeling. The achievement of a flat lens and topologically localized modes is demonstrated, and the tunability of the system allows these properties to hold for a broad range of wavelengths. An ingredient to obtain these effects is the use, suggested here and never attempted before, of concentrated pulsating moments. The important aspect of the proposed method is that states of prestress can be easily removed or changed to tune with continuity the propagational characteristics of the medium, so that a new use of vibration channeling and manipulation is envisaged for elastic materials.
@article{bordiga2019prestress, title = {Prestress Tuning of Negative Refraction and Wave Channeling from Flexural Sources}, author = {Bordiga, G. and Cabras, L. and Piccolroaz, A. and Bigoni, D.}, year = {2019}, month = jan, journal = {Applied Physics Letters}, volume = {114}, number = {4}, pages = {041901}, issn = {0003-6951}, doi = {10.1063/1.5084258}, addendum = {(Editor's Pick)}, }